|
Size: 972
Comment:
|
Size: 976
Comment: converted to 1.6 markup
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
| attachment:surface_normal1.jpg | {{attachment:surface_normal1.jpg}} |
| Line 12: | Line 12: |
| (V0, V1, and V2), which are ordered in such a way that the normalized cross-product of vector --''V0''``''V1''-- and vector --''V0''``''V2''-- gives the outward normal of the face. |
(V0, V1, and V2), which are ordered in such a way that the normalized cross-product of vector __''V0''``''V1''__ and vector __''V0''``''V2''__ gives the outward normal of the face. |
A surface normal is by definition a three-dimensional vector which is perpendicular to that surface.
The surfaces (white or pial) generated by FreeSurfer are represented in the form of triangular meshes. In this case, a normal vector can be computed for each face or triangle of a given surface mesh, using the vector cross-product of two edges of the face triangle.
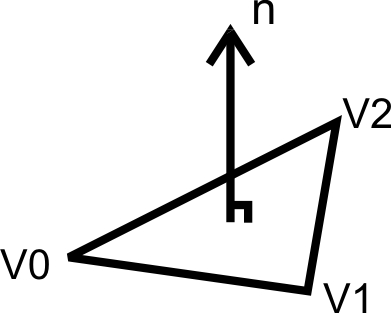
In addition, the surfaces generated by FreeSurfer are considered to be oriented, and the direction of the surface normal follows the right-hand rule. In particular, each triangle face has three vertices (V0, V1, and V2), which are ordered in such a way that the normalized cross-product of vector V0V1 and vector V0V2 gives the outward normal of the face.
By convention, FreeSurfer defines the normal vector at a surface vertex as the normalized average of the normal vectors at all faces sharing this vertex.