Thickness reproducibility

Author: Xiao Han (see also: XiaoNotes)

This wiki page describes how to compute the difference map of cortical thickness from two repeated scans of the same subject, and how to compute the overall statistics from a group of such repeated scans. This computation is needed in validation studies of cortical thickness measurement using FreeSurfer.

Note: The method described here is deprecated and was used on independently processed data (cross sectionally).

In the following, we assume that each subject has two repeated scans, for example, 1001 and 1001a are two scans for the first subject. We also assume that recon-all has been completed for all the data. The thickness reliability study will consist of the following 4 steps.

Step 1. Compute the linear alignment between the two repeated scans of each subject.

Taking 1001 and 1001a as an example, we use FLIRT for the linear registration, and the command line is: 

fsl_rigid_register -i $SUBJECTS_DIR/1001/mri/orig.mgz \
  -r $SUBJECTS_DIR/1001a/mri/orig.mgz \
  -o $SUBJECTS_DIR/1001a/mri/orig_o_to_a.mgz \
  -dof 9 -cost corratio \
  -ltamat $SUBJECTS_DIR/1001/mri/transforms/1001_to_1001a.lta

"1001_to_1001a.lta" is the output registration file that will be used later. The output $SUBJECTS_DIR/1001a/mri/orig_o_to_a.mgz can be used to check the registration accuracy.

Step 2. Compute the thickness difference map for each subject.

Taking again 1001 as an example, the command line is: 

mris_thickness_diff -xform $SUBJECTS_DIR/1001/mri/transforms/1001_to_1001a.lta \
  -src_type curv \
  -out $SUBJECTS_DIR/1001/surf/lh.thickness_diff.mgh \
  -nsmooth 0 \
  -abs -S 1001 \
  -L $SUBJECTS_DIR/1001/surf/lh_thickness_diff.log \
  $SUBJECTS_DIR/1001/surf/lh.white \
  $SUBJECTS_DIR/1001/surf/lh.thickness \
  $SUBJECTS_DIR/1001a/surf/lh.white \
  $SUBJECTS_DIR/1001a/surf/lh.thickness

The above command need be run for the right hemisphere (rh) as well.

Many options are optional.

The last four arguments are the two surfaces and the two thickness maps. Note that the computed thickness difference map is sampled on the first surface, $SUBJECTS_DIR/1001/surf/lh.white in this case. This means the number of entries in the output curvature file matches the number of vertices of the first surface.

The above two steps complete the thickness difference computation for an individual subject, and the output difference map indicates the relative error in the thickness measurement along the cortical surface of the individual subject.

To compute the group-wise statistics of such thickness error, the thickness difference (or error) maps need be resampled to a common template, and then the error statistics can be computed point-wise along the template surface. This re sampling requires a nonlinear alignment across different subjects, which is provided by the spherical registration in FreeSurfer. Different choices of the template is possible. One straightforward option is to simply select one subject from the group as the template.

In the following, we assume the subject 1001 is chosen as the template. The group analysis requires the next two steps.

Step 3. Resample the thickness difference map for each subject to the common template.

Taking subject 1002 as an example, and the command line is: 

mri_surf2surf --srcsubject 1002 \
  --sval $SUBJECTS_DIR/1002/surf/lh.thickness_diff.mgh \
  --trgsubject 1001 \
  --tval $SUBJECTS_DIR/groupstudy/1002_lh_thicknes_diff_resampled_to_1001.mgh \
  --hemi lh \
  --surfreg sphere.reg

The output is the resampled difference map $SUBJECTS_DIR/groupstudy/1002_lh_thicknes_diff_resampled_to_1001.mgh. The same computation can be done for the right-hemisphere (rh) as well.

Step 4. Compute the group-wise mean and std of the thickness differences at every vertex of the template surface

Assuming all the thickness difference maps are resampled to the same template (surface), the command is: 

mris_surface_stats -mask some_mask.label \
  -nsmooth $N \
  -surf_name $SUBJECTS_DIR/1001/surf/${hemi}.white \
  -out_name $SUBJECTS_DIR/groupstudy/${hemi}_std_${N}.mgh \
  -absmean $SUBJECTS_DIR/groupstudy/${hemi}_absmean_${N}.mgh \
  -mean $SUBJECTS_DIR/groupstudy/${hemi}_mean_${N}.mgh \
  -absstd $SUBJECTS_DIR/groupstudy/${hemi}_absstd_${N}.mgh \
  $SUBJECTS_DIR/groupstudy/1???_${hemi}_thickness_diff_resampled_to_1001.mgh

This command computes the mean and std of both the signed and unsigned thickness differences and outputs the results to different files as specified by the different options. The user can define the hemisphere "${hemi}$", and the number of smoothing iterations "$N" applied to the input difference maps. The other options are:

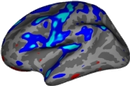
The statistical maps can be displayed on the template subject's surfaces, which can be used to visualize the spatially varying pattern of the thickness measurement variability.

thickdiffmap script

This downloadable script: thickdiffmap is a utility which wraps the four preceding steps into a single script. An example of its usage is: 

set templsubj=(APN05T650_2)
set hemi=(lh)

rm -f resampled

./thickdiffmap APN01R650_4 APN01R650_5 $templsubj $hemi 1 2 3
./thickdiffmap APN02G650_4 APN02G650_4 $templsubj $hemi 1 2 3
./thickdiffmap APN03L650_3 APN03L650_4 $templsubj $hemi 1 2 3
./thickdiffmap APN04E650_2 APN04E650_3 $templsubj $hemi 1 2 3
./thickdiffmap APN05T650_2 APN05T650_3 $templsubj $hemi 1 2 3

./thickdiffmap unused unused $templsubj $hemi 4

Here, five subjects each have a pair of scans. One of the subjects, 'templsubj', is chosen as the common template subject to which the results are mapped. The file resampled is created during the 3'rd step, and contains the difference maps for the group (in this example, a group of five subject pairs).

ThicknessRepeatibility (last edited 2011-01-03 19:11:37 by MartinReuter)